Nelygybių sistema yra sprendimas. Linijinės nelygybės sistema

Nelygybė ir nelygybė yra viena ištai, kas vyksta vidurinėje mokykloje algebra. Sudėtingumo lygiu tai nėra sunkiausia, nes joje yra paprastų taisyklių (apie juos šiek tiek vėliau). Paprastai studentai gali lengvai išspręsti nelygybės sistemą. Taip yra dėl to, kad mokytojai tiesiog "moko" savo moksleivius šia tema. Ir jie negali tai padaryti, nes ateityje jis bus nagrinėjamas naudojant kitus matematinius kiekius, taip pat patikrintas OGE ir USE. Skoliniuose vadovėliuose nelygybės ir nelygybės tema yra išsamiai apibūdinta, taigi, jei jūs ketinate ją išnagrinėti, tai geriausia juos taikyti. Šiame straipsnyje tik persipina didžiosios medžiagos, ir jame gali būti tam tikrų praleidimų.

Nelygybės sistemos samprata

Jei kreipiatės į mokslinę kalbą, galite tai duotiapibrėžti "sistemos nelygybę" koncepciją. Tai toks matematinis modelis, kuris yra keletas skirtumų. Nuo šio modelio, žinoma, ji turi sprendimą, ir savo gebėjimą veikti kaip bendros atsakyti už visų sistemos nelygybę pasiūlytų darbą (paprastai tai ir rašyti, pavyzdžiui: "Išspręskite nelygybę sistemą 4 x + 1> 2 ir 30 - X > 6 ... "). Tačiau prieš pradedant tipų ir metodų priėmimo, jums reikia ką nors išsiaiškinti, ką.

Nelygybių sistemos ir lygčių sistema

Dažniausiai studijuoja naują temąyra nesusipratimų. Viena vertus, viskas aišku ir gana norite pradėti spręsti uždavinius, o kita - kai kurie momentai lieka "šešėlyje", tai nėra gerai suprasta. Be to, kai kurie jau įgytų žinių elementai gali būti susipynę su naujais. Dėl šios "sutapimo" dažnai atsiranda klaidų.

Todėl prieš pradėdami analizuoti savotemą, turėtumėte prisiminti apie skirtumus tarp lygčių ir nelygybės, jų sistemų. Norėdami tai padaryti, turime dar kartą paaiškinti, kas yra matematinės sąvokos. Lygtis visada yra lygybė, ir ji visada yra kažkas lygi (matematikos požiūriu šis žodis žymimas ženklu "="). Nelygybė - tai modelis, kuriame yra vienas ar daugiau ar mažesnis, nei kitas, skaičius arba yra teiginys, kad jie nėra vienodi. Taigi, pirmojoje byloje tinkama kalbėti apie lygybę, o antroje byloje, tačiau akivaizdu, kad iš pavadinimo gali kilti nelygybė iš pradinių duomenų. Sistemos lygtyse ir nelygybės praktiškai nesiskiria vienas nuo kito, o jų sprendimo būdai yra vienodi. Vienintelis skirtumas yra tai, kad pirmuoju atveju mes naudojame lygybes, o antrojoje nelygybė yra naudojama.

Nelygybės tipai

Yra dviejų rūšių nelygybė: skaitinė ir nežinomas kintamasis. Pirmasis tipas yra numatyta kiekis (skaičius), nelygus vienas kitam, pavyzdžiui 8> 10. Antra - šioje nelygybės, kurių sudėtyje yra nežinomas kintamasis (pažymėtą pagal abėcėlės raidė, dažniausiai X). Šis kintamasis reikalauja jo išvados. Priklausomai nuo to, kiek iš jų, matematinio modelio žymūs nelygybės su vienu (sudaro nelygybės sistemą su vienu kintamuoju) arba daugiau kintamųjų (sudaro nelygybės sistema su kelių kintamųjų).

Paskutinės dvi rūšys, atsižvelgiant į jų statybos laipsnį irsprendimų sudėtingumo lygis yra padalintas į paprastą ir sudėtingą. Paprastas taip pat vadinamas linijine nelygybe. Jos, savo ruožtu, yra suskirstytos į griežtus ir griežtus. Tiksliau tariant "pasakykite", kad viena vertė privalo būti mažesnė ar didesnė, taigi gryna jos forma yra nelygybė. Galime pateikti keletą pavyzdžių: 8 x + 9> 2, 100 - 3 x> 5 ir tt Netiesiogiai priskiriama ir lygybė. Tai reiškia, kad viena vertė gali būti didesnė arba lygi kitam vertė (Registruotis "≥") arba mažesnis arba lygus kitam vertė (ženklas "≤"). Daugiau linijiniai nelygybė kintamojo nėra ant kvadratinės šaknies, nėra dalijama nieko, kuris yra, kodėl jie vadinami "paprastas". Kompleksiniai yra nežinomi kintamieji, kurių nustatymas reikalauja daugiau matematinių operacijų. Jie dažnai rasti kvadrato, kubo ar pagal šaknis gali būti modulinė, prisijunkite, trupmeninė ir tt Bet kadangi mūsų užduotis yra suprasti, kaip spręsti sistemų skirtumų poreikį, mes kalbame apie linijinių nelygybės sistema. Tačiau prieš tai turėtumėte pasakyti keletą žodžių apie jų savybes.

Nelygybės ypatybės

Nelygybei būdingos tokios nuostatos:

1. Nelygybės ženklas pasikeičia, jei operacija naudojama norint pakeisti atgalines puses (pvz., Jei t₁ ≤ t₂, tada t₂ ≥ t₁)
2. Abiejose nelygybės dalyse galima pridėti prie to paties numerio (pavyzdžiui, jei t₁ ≤ t₂, tada t₁ + skaičius ≤ t₂ + numeris).
3. Dvi ar daugiau nelygybių, turinčių vienos krypties ženklus, leidžia pridėti jų kairę ir dešinę puses (pavyzdžiui, jei t₁ ≥ t₂, t₃ ≥ t₄, tada t₁ + t₃ ≥ t₂ + t₄)
4. Abiejose nelygybės dalyse galima pailginti arba padalyti į tą patį teigiamą skaičių (pavyzdžiui, jei t₁ ≤ t₂ ir skaičius ≤ 0, tada skaičius t₁ ≥ skaičius · t₂)
5. Dvi ar daugiau nelygybių, turinčių teigiamus terminus ir vienos krypties požymį, leidžia vienas kitą padauginti (pvz., Jei t₁ ≤ t₂, t₃ ≤ t₄, t₁, t₂, t₃, t₄ ≥ 0 tada t₁ · T₃ ≤ t₂ · T₄)
6. Abiejose nelygybės dalyse galima pailginti arba padalyti į tą patį neigiamą skaičių, tačiau nelygybės ženklas pasikeičia (pavyzdžiui, jei t₁ ≤ t₂ ir skaičius ≤ 0, tada skaičius t₁ ≥ skaičius · t₂)
7. Visi nelygybes turi transitizavimo savybes (pvz., Jei t₁ ≤ t₂ ir t₂ ≤ t₃, tada t₁ ≤ t₃)

Dabar, išnagrinėję pagrindines teorijos nuostatas, susijusias su nelygybe, galime tiesiogiai tiesiogiai apsvarstyti taisykles, skirtas jų sistemoms spręsti.

Nelygybės sistemų sprendimas. Bendra informacija. Sprendimai

Kaip jau minėta, sprendimas yraKintamojo reikšmės, tinkamos visoms nurodytos sistemos nelygybėms. Nelygumų sistemų sprendimas yra matematinių veiksmų, kurie ilgainiui gali padėti išspręsti visą sistemą, arba įrodyti, kad nėra jokių sprendimų. Tokiu atveju pasakykite, kad kintamasis nurodo tuščią skaitmeninį rinkinį (parašytas taip: raidė, žymintis kintamąjį ∈ (ženklas "priklauso") ø (ženklas "tuščias"daug "), pavyzdžiui, X ∈ Ø (skaityti taip:" kintamasis "X" priklauso tuščias Set ") Yra keletas būdų, kaip išspręsti sistemų skirtumų: .. grafinis, algebrinė, reikėtų pažymėti metodas pakeistas, kad jie susiję su matematiniais modeliais, kad turi keletą nežinomų kintamųjų.Jei yra tik vienas, tinkamas intervalų metodas.

Grafinis metodas

Leidžia išspręsti nelygybės sistemą keliomisnežinomos reikšmės (nuo dviejų ir daugiau). Dėka šio metodo, linijinių nelygybės sistema išspręsta gana lengvai ir greitai, todėl yra labiausiai paplitęs būdas. Taip yra todėl, kad grafiko konstrukcija sumažina matematinių operacijų rašymo kiekį. Ypač malonus tampa šiek tiek išsiblaškęs nuo rankenos, pasiimti pieštuką su liniuote ir pereikite prie tolesnių veiksmų su jais, kai daroma daug darbų ir nori šiek tiek įvairovės. Tačiau šis metodas yra ne taip, kaip kai kurie iš to, kad mes turime atitrūkti nuo darbo ir pereiti savo protinę veiklą brėžinyje. Nepaisant to, tai yra labai veiksmingas būdas.

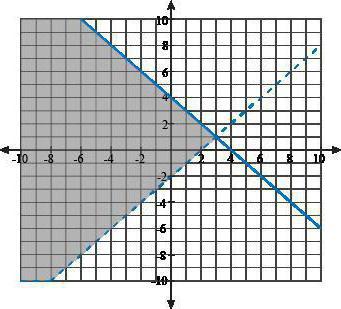
Nustatyti nelygybės sistemą suNaudojant grafinį metodą, kiekvieną nelygybę būtina perkelti į kairę. Ženklai yra atvirkščiai, teisingai turėtų būti parašyta nulis, tada kiekvieną nelygybę turite rašyti atskirai. Dėl to nelygybes gaunančios funkcijos. Po to galite gauti pieštuką ir valdiklį: dabar reikės parengti kiekvienos gaunamos funkcijos grafiką. Visų skaičių rinkinys, kuris bus jų sankirtos intervalas, bus nelygybės sistemos sprendimas.

Algebrinis metodas

Tai leidžia spręsti nelygybes su dviem sistemomisnežinomi kintamieji. Be to, nelygybė turi turėti tą patį nelygybės ženklą (tai yra, jame turi būti tik ženklas "daugiau" arba tik ženklas "mažiau" ir kt.). Nepaisant apribojimų, šis metodas taip pat yra sudėtingesnis. Jis taikomas dviem etapais.

Pirmasis reikalauja atsikratyti aktovienas iš nežinomų kintamųjų. Pirmiausia turite jį pasirinkti, tada patikrinkite numerių buvimą prieš šį kintamąjį. Jei jie nėra (tada kintamasis atrodys viena raidė), tada niekas nepasikeis, jei yra (tipo kintamojo, pavyzdžiui, taip - 5y ir 12y), tada jūs turite įsitikinti, kad kiekvienas skaičius nelygybė prieš pasirinktą kintamasis buvo tas pats. Norėdami tai padaryti, dauginti kiekvieną nelygybę narį bendru faktorius, pavyzdžiui, jei pirmasis nelygybė įrašyti 3Y, 5Y o antrasis, būtina visų pirmą nelygybė, padauginta iš 5 narių, o antrasis - ant 3. Pereikite 15y ir 15y, atitinkamai.

Antrasis sprendimo etapas. Mums reikia perkelti kairę kiekvienos nelygybės pusę į dešinę pusę, pakeisti kiekvieno termino ženklą į priešingą, į dešinę, parašyti nulį. Tada ateina įdomiausia: atsikratyti pasirinkto kintamojo (kitaip tai vadinama "sutrumpinimu"), nulūžus nelygybes. Mes gauname nelygybę su vienu kintamuoju, kurį reikia išspręsti. Po to turėtumėte daryti tą patį tik su kitu nežinomu kintamu. Gauti rezultatai bus sistemos sprendimas.

Pakeitimo metodas

Leidžia išspręsti nelygybės sistemą esantgebėjimas įvesti naują kintamąjį. Paprastai šis metodas naudojamas, kai netiesioginis kintamasis vienoje nelygybės sąlygoje yra pakeltas į ketvirtąją galią, o kitu terminu turi kvadratą. Taigi, šis metodas skirtas sumažinti nelygybės lygį sistemoje. Ėminio nelygybė x⁴ - x² - 1 ≤ 0 tokiu būdu yra sprendžiamas taip. Įvestas naujas kintamasis, pvz., T. Jie rašo: "Tegul t = x²", tada modelis perrašomas nauja forma. Mūsų atveju mes gauname t² - t - 1 ≤0. Ši nelygybė turi būti išspręsta intervalu metodu (apie tai šiek tiek vėliau), tada vėl į kintamąjį X vėl, tada padaryti tą patį su kita nelygybė. Gauti atsakymai bus sistemos sprendimas.

Intervalo metodas

Tai yra lengviausias būdas išspręsti sistemasnelygybė, tuo pat metu ji yra universali ir plačiai paplitusi. Jis naudojamas vidurinėje mokykloje ir net aukštojoje mokykloje. Jo esmė yra tai, kad studentas ieško nelygybės intervalų skaičiaus eilutėje, kuri yra užrašyta užrašinėje (tai nėra grafas, o tik paprastoji eilutė su skaičiais). Kai nelygybių intervalai susikerta, randamas sistemos sprendimas. Jei norite naudoti intervalo metodą, turite atlikti šiuos veiksmus:

1. Visi kiekvienos nelygybės sąlygos yra perkeltos į kairę, žymėjimo pasikeitimas (nulis rašomas dešinėje).
2. Nelygybės išsiskiria atskirai, nustatomas kiekvieno iš jų sprendimas.
3. Numerių eilutėje yra nelygumų sankirtos. Visi skaičiai šiuose susikirtimuose bus sprendimas.

Kuris būdas naudoti?

Akivaizdu, kad atrodo, kad yra lengviausias irpatogu, bet yra atvejų, kai užduotis reikalauja tam tikrą metodą. Dažniau nei ne, jie parašyta, kad reikia spręsti arba per grafiką arba intervalais. Algebrinis metodas keitimą ir retai naudojami arba nenaudojami ne visi, nes jie yra sudėtingi ir painūs, o taip pat didesnis taikymas sprendžiant sistemų lygtis, o ne skirtumų, todėl turėtų būti naudojamas atkreipti grafikus ir intervalus. Jie priima aiškumą, kuris negali bet prisidėti prie veiksmingo ir greito elgesio matematinių operacijų.

Jei kažkas neveikia

Studijuodami algebros temą,Žinoma, jos supratimas gali būti problemų. Ir tai yra normalu, nes mūsų smegenys yra suprojektuoti taip, kad tuo metu negalėtų suprasti sudėtingos medžiagos. Dažnai jums reikia perskaityti pastraipą, padėti mokytojui ar praktikuoti tipiškų užduočių sprendimą. Mūsų atveju, pavyzdžiui, jie atrodo taip: "Nustatykite nelygybių sistemą 3 x + 1 ≥ 0 ir 2 x - 1> 3". Taigi, asmeninis troškimas, pagalba iš išorės žmonių ir praktika padeda suvokti bet kokią sudėtingą temą.

Pertvarkymas?

Ir rezhebnik taip pat yra labai geras, bet neuž namų darbų sukčiavimą ir savigarbą. Jie gali rasti nelygybės sistemas su sprendimu, pažvelgti į juos (kaip į šablonus), pabandyti suvokti, kaip tirpalo autorius įveikė užduotį, ir tada bandykite tai padaryti savarankiškai.

Išvados

Algebra yra vienas iš sudėtingiausių dalykųmokykla Na, ką aš galiu padaryti apie tai? Matematika visada buvo tokia: ji tampa lengvai, bet kam sunku. Tačiau bet kokiu atveju reikėtų prisiminti, kad bendrojo lavinimo programa yra sukurta taip, kad bet kuris studentas galėtų tai spręsti. Be to, turime nepamiršti daugybės padėjėjų. Kai kurie iš jų buvo paminėti aukščiau.